കണക്കിനെ പേടിക്കേണ്ട: മനസ്സിലാക്കിയാൽ ഇത്രേയുള്ളൂ

രണ്ട് കോണുകൾ 45 ഡിഗ്രി വീതം ഉള്ള ത്രികോണത്തിന്റെ പേരെന്ത്? ഈ ചോദ്യത്തിന് സമപാർശ്വത്രികോണം (isosceles triangle) എന്നു പറയാൻ ഓർമശക്തി മാത്രം മതി. എന്നാൽ, രണ്ടു കോണുകൾ 45 ഡിഗ്രി വീതമുള്ള ത്രികോണം മട്ടത്രികോണമാണോ എന്ന ചോദ്യത്തിന്റെ ഉത്തരം കണ്ടെത്താൻ കുറച്ചു യുക്തി പ്രയോഗിക്കണം. കോണുകളുടെ തുക 180 ആണെന്ന മുന്നറിവും മൂന്നാമത്തെ കോണളവ് 90 ഡിഗ്രി ആണെന്ന് കണ്ടു പിടിക്കാനുള്ള ക്രിയാശേഷിയും വേണം.

മനസ്സിലാക്കിയാൽ
ഇത്രേയുള്ളൂ
ഇത്തരത്തിൽ ലളിതമായ ഒട്ടേറെ ആശയങ്ങളിലൂടെ കടന്നു പോകുന്നതാണു ഗണിതപഠനം. ചില ഉദാഹരണങ്ങൾ കൂടി പറയാം. ഒരു ത്രികോണത്തിന്റെ 2 കോണുകൾ തുല്യമാണെങ്കിൽ അവയ്ക്കെതിരെയുള്ള വശങ്ങളും തുല്യമായിരിക്കും എന്നറിയാമല്ലോ. ഇതിന്റെ അടുത്ത പടിയാണു കോണളവുകൾ തുല്യമല്ലെങ്കിൽ എന്തു സംഭവിക്കും എന്ന ചോദ്യം. അതൊരു മട്ടത്രികോണമാണെങ്കിൽ കാര്യങ്ങൾ എളുപ്പമാണ്. ഒരു മട്ട ത്രികോണത്തിന്റെ ഒരു കോൺ 30 ഡിഗ്രി ആണെന്നിരിക്കട്ടെ, അതിനെതിരെയുള്ള വശം കർണത്തിന്റെ പകുതി നീളമുള്ളതായിരിക്കും. കേൾക്കുമ്പോൾ ഒരു കൗതുകം തോന്നുന്നില്ലേ? ഇതിനെയാണ് സൈൻ 30 = 1/2 എന്ന് പറയുന്നത്. ഇത്തരത്തിൽ മട്ടത്രികോണത്തിന്റെ വശങ്ങൾ തമ്മിലുള്ള ബന്ധത്തിൽ തുടങ്ങുന്നതാണ് ത്രികോണമിതി. അതിൽ പറയുന്ന മറ്റൊരു കാര്യമുണ്ട്. ഏതൊരു ത്രികോണത്തിന്റെയും പരിവൃത്ത വ്യാസം (Diameter of Circumcircle) കാണാൻ ഏതെങ്കിലും ഒരു വശത്തിന്റെ നീളത്തെ അതിന്റെ എതിരെയുള്ള കോണിന്റെ സൈൻ വില എടുത്ത് ഹരിച്ചാൽ മതി. ത്രികോണമിതിയും അത്ര പേടിക്കാനില്ലെന്നു മനസ്സിലായില്ലേ..?

പരസ്പരബന്ധം
പരമപ്രധാനം
പരിവൃത്ത വ്യാസത്തെക്കുറിച്ചു പറഞ്ഞപ്പോഴാണ് അന്തർ വൃത്തത്തെ (Incircle) ഓർത്തത്. ത്രികോണങ്ങളുടെ അന്തർവൃത്ത ആരത്തിനും (Radius of incircle) ലളിതമായ ഒരു സൂത്രവാക്യമുണ്ട്. അതിന്റെ വിസ്തീർണത്തെ ചുറ്റളവിന്റെ പകുതി കൊണ്ട് ഹരിച്ചാൽ മതി. ഒരു സമാന്തര ശ്രേണിയുടെ ബീജഗണിത രൂപം 3n+1 ആണെങ്കിൽ അതിന്റെ പൊതു വ്യത്യാസം nന്റെ ഗുണകമായ (Coefficient) 3 ആണ്. ഒരു സമാന്തര ശ്രേണിയുടെ മധ്യപദം കാണാൻ രണ്ടറ്റങ്ങളിലുമുള്ള പദങ്ങൾ കൂട്ടി പകുതിയാക്കിയാൽ മതി. മധ്യപദത്തെ എണ്ണം കൊണ്ട് ഗുണിച്ചാൽ ശ്രേണിയുടെ തുകയും കിട്ടും. ഒരു വൃത്തത്തിന്റെ സമവാക്യമാണ് x2+y2 =25 എങ്കിൽ അതിന്റെ കേന്ദ്രം (0,0 ) ആണ്. ആരം 5 ആയിരിക്കും. ഒരു ബഹു പദം P(x) ൽ P( 2 ) = 0 ആണെങ്കിൽ x - 2 ഘടകമാണ്. ഒരു രണ്ടാംകൃതി ബഹുപദത്തോട് (Second degree polynomial) അതിലെ , x ന്റെ ഗുണകത്തിന്റെ പകുതിയുടെ വർഗം കൂട്ടിയാൽ അത് ഒരു പൂർണവർഗമാകും.

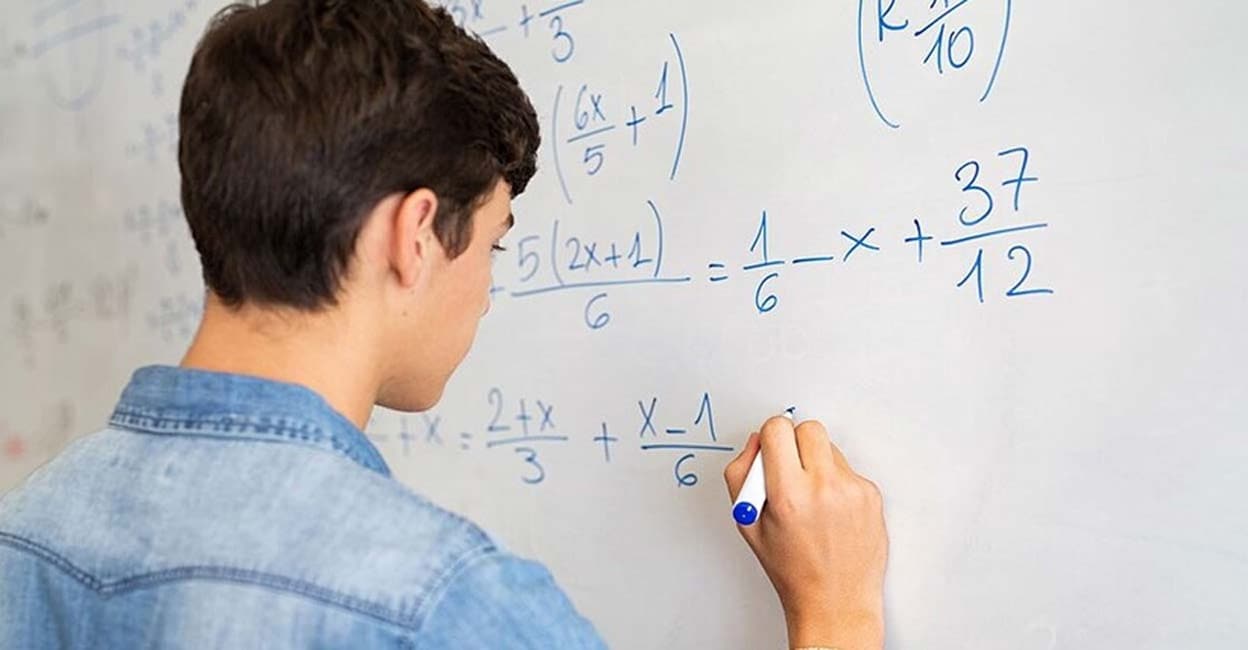
ഒരു പെട്ടിയിൽ 3 പന്തും മറ്റൊരു പെട്ടിയിൽ 4 പന്തുമുണ്ടെന്ന് കരുതുക. ഓരോ പെട്ടിയിൽ നിന്നും ഓരോന്നു വീതമെടുത്ത് ജോഡികളാക്കിയാൽ 3x 4 = 12 വ്യത്യസ്ത തരത്തിൽ ജോഡികളാക്കാം.
ഏതൊരു സ്തൂപികയുടെയും (Pyramids) വ്യാപ്തം പാദപരപ്പളവിന്റെയും (Base area) ഉയരത്തിന്റെയും ഗുണനഫലത്തിന്റെ 1/3 ആണ്. പുറത്തുനിന്ന് ഒരു വൃത്തത്തിലേക്ക് രണ്ട് തൊടുവരകൾ (Tangents) വരച്ചാൽ ഒരേ നീളമായിരിക്കും. ഒരു അർധവൃത്തത്തിലെ കോൺ എപ്പോഴും മട്ട കോണാണ്. ഒരു വരയുടെ 3 ബിന്ദുക്കളാണ് A, B, C എങ്കിൽ AB, BC എന്നീ രണ്ട് ഭാഗങ്ങൾക്കും ഒരേ ചരിവ് ആയിരിക്കും. ഇങ്ങനെ ഗണിത തത്വങ്ങളെ കൗതുകക്കണ്ണുകളിലൂടെ കണ്ടു നോക്കൂ, നിങ്ങൾ ഇഷ്ടപ്പെടും. ഇതു പോലെ പരീക്ഷയെയും കാണുക. നിങ്ങൾ കണ്ട കൗതുകങ്ങൾ പകർത്തിവയ്ക്കാൻ ഒരവസരം ആയി കണ്ടാൽ മതി. എങ്കിൽ സമ്മർദം പകുതി കുറയ്ക്കാം.

കണക്കുകൂട്ടി എഴുതാം
29 ചോദ്യങ്ങൾ ഉണ്ടാകും. ആകെ 110 മാർക്ക്. എന്നാൽ 21 ചോദ്യങ്ങൾക്ക് ഉത്തരമെഴുതിയാൽ മതി. അതായത് 80 മാർക്കിന്. അതിൽ 70 കിട്ടിയാൽ A+ ആയി. 60 കിട്ടിയാൽ A യും. ബുദ്ധിമുട്ടേറിയ ചോദ്യങ്ങൾ മാറ്റി നിർത്തിയാലും ഉയർന്ന ഗ്രേഡുകൾ നേടാം എന്നർഥം. അപ്പോൾ ജയിക്കുക എന്നത് നിസ്സാരമാണ്. മുഴുവൻ CE മാർക്ക് ലഭിച്ച ഒരു കുട്ടിക്ക് 80ൽ 10 മാർക്ക് നേടിയാൽ പോലും ജയിക്കാം. അതിന് സ്ഥിരമായി വരുന്ന നാലോ അഞ്ചോ ചോദ്യങ്ങൾ തന്നെ ധാരാളം. വൃത്തവുമായി ബന്ധപ്പെട്ട 3 നിർമിതികൾ, മധ്യമം കാണാൻ ഉള്ള ഒന്നോ രണ്ടോ ചോദ്യങ്ങൾ എന്നിവ ഉറപ്പ്. കണക്കുപരീക്ഷയെ പേടിക്കുകയേ വേണ്ട എന്നാണ് പറഞ്ഞുവന്നത്.